Biostatistics Formulas

Part 1: The formulas

Part 2: Explanation of the formulas

---

Formulas & Tables

	Disease +	Disease –
Test +	true positive (TP) a	False negative (FN) b	a+b	PPV = a/(a+b)
Test –	False positive (FP) c	True negative (TN) d	c+d	NPV = d/(c+d)
	a+c	b+d	total
	SN = a/(a+c)	SP = d/(b+d)

For Diagnostic tests	Formula
Sensitivity, SN (true-positive rate)	= TP/ (TP +FN) which is a/(a+c)
Specificity, SP (true-negative rate)	= TN/ (TN + FP) which is d/(b+d)
Positive predictive value (PPV)	= TP / (TP + FP), which is a/(a+b)
Negative predictive value (NPV)	= TN / (TN + FN), which is d/(c+d)
Incidence rate	= # of new cases / population at risk. *for a specific time period
Prevalence	= # of existing cases ( / population at risk. *for current period of time
Accuracy	= (TP+TN)/total. The probability of correctly identifying someone as TN or TP.

---

4×4 Contingency table

	Event +	Event –
Exposed or treatment group	a	b	a+b
Unexposed or control group	c	d	c+d
	a+c	b+d	total

---

For Quantifying Risk & Therapeutic Efficacy	Formula
Odds ratio (OR)	ad/ bc
Relative risk (RR)	[a/(a+b)] / [c/(c+d)] i.e. treatment or exposed event rate/ control or unexposed event rate
Relative risk reduction (RRR)	1 – RR. ARR/ control rate
Absolute risk (AR)	[a/(a+b)] – [c/(c+d)]
Absolute risk reduction (ARR)	control rate – treatment rate
Absolute risk increase (ARI)	treatment rate – control rate
Absolute risk percent (ARP)	(RR-1)/RR. Also = (ARI/treatment rate) x 100
Number needed to treat (NNT)	1/ ARR
Number needed to harm (NNH)	1/ ARI

Explanation of Formulas

---

Sensitivity

The quality of a diagnostic test can be determined by its sensitivity and specificity.

Sensitivity tells us how well a test identifies people with the disease. A highly sensitive test makes a great screening tool because it will detect most of the affected individuals in a population. The sensitivity of a test can also be referred to as the true positive rate.

SN = TP/ (TP +FN).

---

Specificity

Specificity tells us how well a test identifies people without the disease. A highly specific test will more effectively rule out those who don’t have a particular disease. The specificity of a test can also be referred to as the true negative rate.

SP = TN/ (TN + FP)

---

Prevalence

Prevalence is the amount of people in the population who are disease positive over the total population.

Prevalence (P) & Predictive value

PPV = positive predictive value, NPV = negative predictive value

↑P = ↑PPV and ↓NPV

↓P = ↓PPV and ↑NPV

---

Odds ratio

The Odds ratio tells us the odds of an outcome (e.g. disease) occurring in the exposed group compared to it occurring in the non-exposed group. The odds ratio is typically used to evaluate case control studies. Note: ossa od disease in the exposed group = a/b, meaning exposed with disease (a) divided by exposed without disease. Odds of disease in the non-exposed group = c/d. We do this, because odds is the comparison of an outcome occurring vs. it not occurring.

OR = (a/b) / (c/d) = (ad)/(bc)

Relative Risk

The Relative risk tells us risk of an outcome (e.g. disease) in the exposed group compared to non-exposed group. The relative risk is typically used to evaluate cohort studies. Note: risk in of disease in the exposed group = a/(a+b), meaning those exposed with the disease divided by all those who were exposed. Risk in the non-exposed group is c/(c+d). We do this, because risk is the chance the outcome of interest will occur compared to the chance of all possible outcomes occurring.

RR = [a/(a+b)] / [c/(c+d)]

The odds ratio may approximate the relative risk

It is possible for the relative risk to approach the odds ratio i.e. RR ~ OR.

RR = [a/(a+b)] / [c/(c+d)] = (a/b) / (c/d) = ad/bc = OR. If a << b and c << d.

This occurs when a disease is rare i.e. when there is low prevalence of disease.

What does the relative risk mean?

RR = 1 means that there is no relationship between the exposure and the outcome (e.g. disease).

RR > 1 means that there is a positive relationship between the exposure and the outcome (e.g. disease). This means that the exposure is associated with an increased risk of disease.

RR < 1 means that there is a negative relationship between the exposure and the outcome. In this case, the exposure is associated with a decreased risk of disease.

---

Test Cut-off values

Changing the cut-off value needed for a test to be positive, HbA1c >6.5 is positive, will change many measures (TN, TP, SN, SP, PPV, NPV). Many questions of boards will ask which direction theses measures will change based on whether the cut-off is lowered or increased.

Higher cut-off leads to increased SP, TN, and NPV i.e. all the “negatives” because a higher cut-off will result in more people without disease testing positive. Where as lower cut-off leads to increased SN, TP, and PPV i.e. all the “positives”, because a lower cut-off value will result in more of the positive test results being due to those who really do have disease.

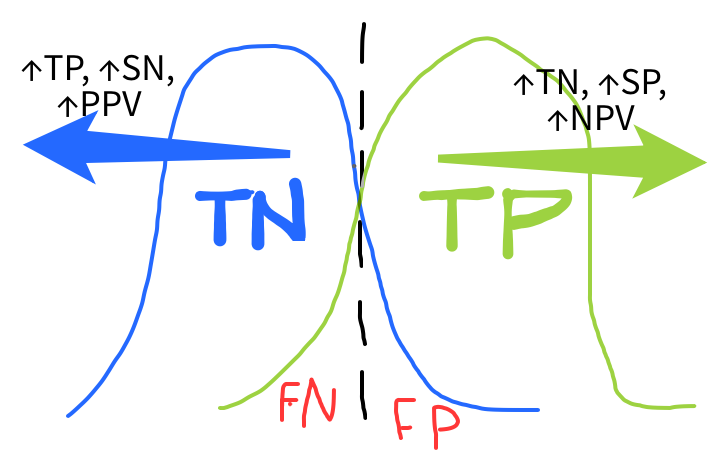
For example, if the blood pressure cut-off to diagnose hypertension is reduced to 120/80 then we will catch everyone with hypertension, i.e. increase TP, PPV and SN. However, we will have many more false positives, so higher TN, SP and NPV.

	Disease +	Disease –
Test +	true positive (TP) a	False negative (FN) b	a+b	PPV = a/(a+b)
Test –	False positive (FP) c	True negative (TN) d	c+d	NPV = d/(c+d)
	a+c	b+d	total
	SN = a/(a+c)	SP = d/(b+d)

Using the table, if a is increased i.e. more positive tests because the cut-off for a positive test is lowered, then ↑TP (=a) and ↑PPV (= a/(a+b)) and ↑SN (=a/(a+c)).

Similarly, if the cut-off value needed for a positive test is increased, then less a and more d. So, ↑TN (=d) and ↑NPV (=d/(c+d)) and ↑SP (=d/(b+d).

---

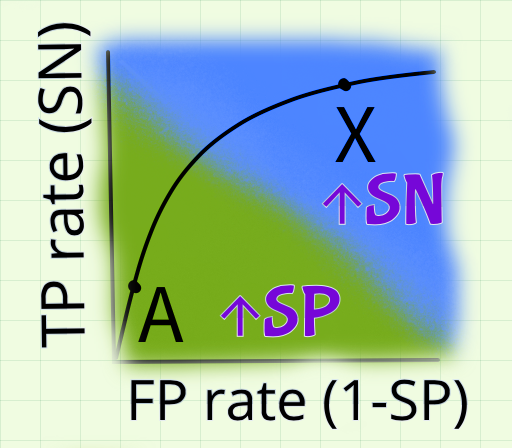
Receiver operative curve (ROC)

This curve shows how test SN and SP change with changing cut-off values. Here, X is a low cut-off approaching 0%, and A is the higher cut-off which approaches 100%. Specificity (SP) is highest at A, and Sensitivity (SN) is highest at X.